

Oriented to Master, PhD students and young researchers in Mathematics, Science or Engineering.
Prerequisites: Mathematics and computer programming skills.
3 courses & 5 lectures in a friendly environment for enjoying computational mathematics and applications.

This school is designed for young students, up to master and doctorate level, seeking to acquire skills in the latest trends in mathematical and computational modeling. We place a strong emphasis on practical applications in science and engineering, with a focus on modeling spatiotemporal variations of physical quantities using partial differential equations (PDEs) and related topics such as finite element methods, neural networks and numerical optimization, playing a vital role today in fields like deep learning.
The school is organized into three courses. Two courses will cover the widely used finite element method (FEM) and other emerging techniques such as physically informed neural networks (PINN) for computing numerical solutions of PDEs. The third course will focus on numerical methods for constrained and unconstrained optimization. In these courses, we introduce fundamental mathematical structures, provide illustrative examples, review algorithms, program them using high-level open-source tools, and post-process the solutions for high-quality plotting.
The essential mathematical and computer skills will be standardized in introductory online sessions, with expert proffesors in the field overseeing the entire learning process. The courses will be complemented by five lectures aimed at introducing recent research directions relevant to the field.
The school begins with a phase dedicated to homogenizing the students’ knowledge to help them reach a basic level before the classroom courses begin to develop in Split. It will be designed as 5 online days where students will be able to access material specifically prepared for them to acquire basic math and computer skills. During these days they will have the support and tutoring of the curses instructors, through video meetings and forums in a virtual campus.
In the second week, the School will be held physically on the premises of the University of Split. It will consist on three courses where theoretical lectures will be given and numerous examples, algorithms and exercises will be reviewed. In computer classes, students will be provided with the necessary software to implement the algorithms and analyze the results. The courses will be complemented with lectures where invited professors will stimulate the curiosity of the students, stowing recent research topics related to computational mathematics.
After the end of the classes in Split, the students interested in receiving ECTS credits will submit a final work in small groups related to the school topics. For this, they will be assisted in a final tutoring session.
Participants who complete the course will receive 3 ECTS credits. Evaluations for students interested in credit recognition will be based on daily attendance to the school and a on final offline group work.

The city of Split, Croatia, is served by an international airport which is located approximately 20 km from the city center of Split, on the west side of Kaštela Bay. Regular taxis at Split Airport are available during the airport’s operating hours, with the average cab fare to the center of Split being about 30 euros. Other options for travelling include shuttle bus (Pleso Prijevoz) and local bus, with respective costs of 6€ and 2.5€.
The School will provide students with up to 20 dormitory rooms in the university residence located on the university campus, a 5-minute walk from the Faculty of Science, where the activities will take place. Breakfast and lunch are included.
Up to 20 Students coming either from a SEA-EU University or from any EU Member State or third country associated to the Erasmus+ program can apply for funding through Blended Intensive Program (BIP). This will allow them to get support to attend the classroom week in Split.
Organizer & Speaker: Francisco Ortegón Gallego (Universidad de Cádiz)
Classroom time: 10 hours
Topics:
Freefem++: numerical resolution of PDEs.
Organizers & Speakers: J. Rafael Rodríguez Galván, M. Victoria Redondo Neble (Universidad de Cádiz)
Classroom time: 10 hours
Topics:
Organizer & Speaker: Malte Braack (University of Kiel)
Classroom time: 6 hours lectures, 4 hours exercises
Topics:

Theoretical and numerical analysis of Navier-Stokes equations arising in fluid confinement
In this lecture, we consider the incompressible Navier-Stokes equations with the forcing term assumed to be (non-linearly) dependent on the velocity field. Some applications of this problem will be shown. For the considered problem, we characterize feedback forces fields that are able of confining the fluid flow. We use the Continuous/Discontinuous Finite Element Method with interior penalty terms to solve the resulting nonlinear fourth-order problem. For the associated continuous and discrete problems, we prove the existence of weak solutions and establish the conditions for their uniqueness. Consistency, stability, and convergence of the numerical method are also shown analytically. To validate the numerical model regarding its applicability and robustness, several test cases are carried out.
Split in Split
Splitting methods are well established and widely used techniques for finding approximate solutions of linear DEs of the form u’=(A+B)u. They can be also used for the case of time dependent component B(t). In this lecture I will give a short introduction to this subject on the example of celebrated Strang splitting for possibly time dependant component. I will show, that surpassingly it can be derived from Duhamel (Variation-of-Constant) formula. Based on this approach I will present a new proof of convergence of this scheme and elaborate on the possibilities brought by this approach.Solvable Structures and C-infinity Structures for Differential Equations
We present some new integration methods for ordinary differential equations, based on the existence of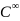 -structures,
a recent generalization of the concept of solvable structure.
Both notions are established in the more general context of the
integrability of involutive distributions Z of vector fields.
Several illustrative examples show how both objects (solvable structures and
-structures,
a recent generalization of the concept of solvable structure.
Both notions are established in the more general context of the
integrability of involutive distributions Z of vector fields.
Several illustrative examples show how both objects (solvable structures and
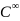 -structures)
can be found and used in practice to obtain exact solutions for
problems modelled by ordinary differential equations.
-structures)
can be found and used in practice to obtain exact solutions for
problems modelled by ordinary differential equations.
Introduction to Asymptotic Methods in Fluid Mechanics
The application of asymptotic analysis to partial differential equations is presented using the example of a fluid flow through a thin pipe that is heated. The expansion of the pipe is considered and the small system parameters are the expansion coefficient of the pipe and the radius of the circular pipe.
Introduction to Symplectic Methods for Hamiltonian Systems
Hamilton’s equations describe the time evolution of a mechanical system defined on a symplectic manifold. Such systems have a wide range of applications from celestial mechanics, rigid body motion to molecular dynamics. When discretizing Hamilton’s equations, one wishes to preserve the geometric properties important for qualitative behavior of the system. In this talk we give a short introduction to symplectic integrators for Hamiltonian systems based on preservation of the symplectic form under the flow of a Hamiltonian vector field. We discuss the symplectic Euler and Stromer-Verlet algorithms as well as composition methods for symplectic maps. We show that these algorithms outperform standard methods in terms of accuracy and stability for long time integrations. These methods are illustrated with several interesting examples from physics.
Universidad de Cádiz, Spain

Universidad de Cádiz, Spain

Universidad de Cádiz, Spain

Kiel University, Germany

University of Split, Croatia

Universidade do Algarve and CMAFcIO, Portugal

Institute of Mathematics of the Polish Academy of Sciences

Universidad de Cádiz, Spain

Uniwersytet Gdańsk, Poland

University of Split, Croatia

Universidad de Cádiz, Spain
Monday 2, 9:00h. Opening (video conference). Introduction to Course 1 (video conference).
10:00h Francisco Ortegón Gallego. Individual work, tutored in forums on the virtual campus
Tuesday 3, 9:00h. Introduction to Course 2 (video conference). J. Rafael Rodríguez Galván & M. Victoria Redondo Neble. Individual work, tutored in forums on the virtual campus
Wednesday 4, 9:00h. Introduction to Course 3 (video conference). Malte Braack. Individual work, tutored in forums on the virtual campus
Thursday 5 and Wednesday 6. Guided exercises.

An insight of mathematical and computational tools for simulation of models from Science and Engineering, specifically those which are written as PDE.
With a first course on the finite element method (FEM) for numerical approximation of PDE, a second one on Artificial Intelligence for learning solutions to PDE, in particular by delving into physically informed neural networks (PINN), and a third course on numerical methods for constrained and unconstrained optimization.
Computer Simulation of PDE Models
Artifical Intelligence
Numerical optimization
Please, complete the following form before the application deadline (in case you are unable to visualize it correctly, you can complete it through this link):
Prof. Sasa Kresic-Juric, sea-eu.comp.math@pmfst.hr.
Department of Mathematics,
Faculty of Science,
University of Split.
Rudjera Boskovica 33.
21000 Split, Croatia.
Phone: +385 21 619 228
Email: sea-eu.comp.math@pmfst.hr

See you in Split!